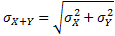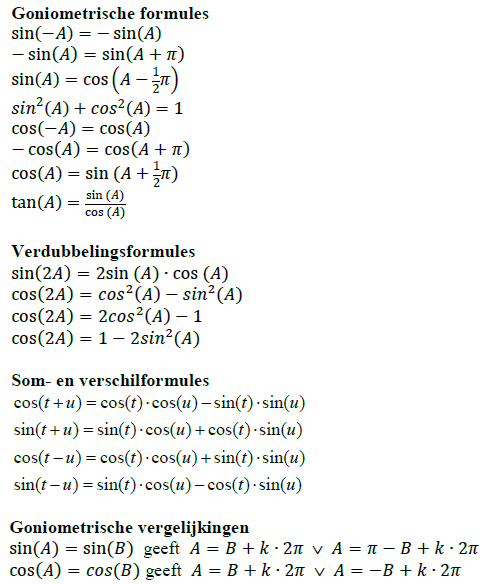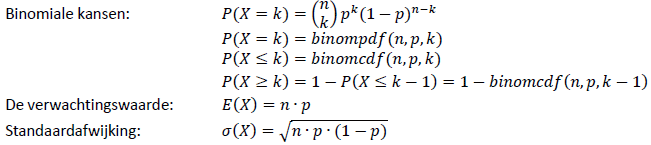| Hoofdstuk 1 | Handige manier om het aantal diagonalen uit te rekenen van een veelhoek:
diagonalen = aantal hoekpunten x (aantal hoekpunten - 3) : 2. |
| Hoofdstuk 2 | Volgorde bij berekeningen
1. werk binnen de haakjes
2. x, : (van links naar rechts)
3. +, - (van links naar rechts)
Breuken vermenigvuldigen
breuk x breuk = (teller x teller) / (noemer x noemer) |
| Hoofdstuk 4 | lineaire woordformules, soms met 2 variabelen
Regels voor het vermenigvuldigen
+ x + = +
+ x - = -
- x + = -
- x - = +
Regels voor het delen
+ : + = +
+ : - = -
- : + = -
- : - = +
Delen door nul is niet toegestaan |
| Hoofdstuk 6 | lineaire formuleskwadratische formulesparabool
Volgorde bij berekeningen
1. werk binnen de haakjes
2. kwadrateren
3. x, : (van links naar rechts)
4. +, - (van links naar rechts) |
| Hoofdstuk 8 | Wegwerken van haakjesa(b + c) = ab + ac
Volgorde bij berekeningen
1. werk binnen de haakjes
2. machtsverheffen
3. x, : (van links naar rechts)
4. +, - (van links naar rechts)
Rekenregels bij machten (alleen toepassen zonder dat onderstaande regels worden gegeven)ap . aq = ap + q
(ap)q = ap . q
(ab)n = an . bn
ap/aq = ap - q |
| Hoofdstuk 9 | oppervlakte(driehoek) = 0,5 . basis . hoogte.
omtrek(cirkel) = pi . diameter.
oppervlakte(cirkel) = pi . straal2.
inhoud(balk) = lengte . breedte . hoogte |
| Hoofdstuk 1 | berg- en dalparabool
Rekenregels met wortels√((a)2) = a√(a) .√(b) = √(ab)√(a)/√(b) = √(a/b) |
| Hoofdstuk 2 | opp(parallellogram) = zijde . hoogte
opp(trapezium) = 0,5 . (a + b) . h
opp(vlieger) = 0,5 . ene diagonaal . andere diagonaal |
| Hoofdstuk 3 | Haakjes wegwerkena(b + c) = ab + ac
(a + b)(c + d) = ac + ad + bc + bd
Merkwaardige producten
(a + b)(a - b) = a2 - b2
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
Regels voor machten
ap . aq = ap + q
(ap)q = ap . q
(ab)n = an . bn
ap/aq = ap - q |
| Hoofdstuk 5 | lineaire formulesrichtingscoëfficiënt = verticaal/horizontaal |
| Hoofdstuk 6 | stelling van Pythagoras: a2 + b2 = c2 (bij rechthoekige driehoeken)
Ontbinden in factoren
ab + ac = a(b + c)
a2 - b2 = (a + b)(a - b)
AB = 0 => A = 0 v B = 0 |
| Hoofdstuk 8 | inhoud(prisma) = opp(grondvlak) . hoogte
inhoud(piramide) = 1/3 . opp(grondvlak) . hoogte
inhoud(kegel) = 1/3 . opp(grondvlak) . hoogte
vergrotingsfactor k = beeld/origineel
lengte(groot) = k . lengte(klein)
opp(groot) = k2 . opp(klein)
inhoud(groot) = k3 . inhoud(klein) |
| Hoofdstuk 1 | lineaire formules opstellenorigineelbeeldformulefunctiefunctiewaardehaakjesnotatie |
| Hoofdstuk 2 | stelling van Pythagoras: a2 + b2 = c2hellingsgetal = (verticale verplaatsing) / (horizontale verplaatsing)tan(hellingshoek) = (Verticale verplaatsing) / (Horizontale verplaatsing)tan(hellingshoek) = hellingsgetaltan-1(hellingsgetal) = hellingshoektan(hoek A) = (overstaande rechthoekszijde van hoek A) / (aanliggende rechthoekszijde van hoek A) |
| Hoofdstuk 3 | f(x) = ax2 + bx + cxtop = (xA + xB) / 2A . B = 0 geeft A = 0 v B = 0snijpunt x-as bepalen: f(x) = 0snijpunt y-as bepalen: f(0) berekenenabc-formule: x = (-b +/- √(D)) / 2a, met D = b2 - 4ac |
| Hoofdstuk 4 | procenuele toename/afname = (nieuw - oud)/oud x 100% |
| Hoofdstuk 5 | Haakjes wegwerkena(b + c) = ab + ac(a + b)(c + d) = ac + ad + bc + bd(ab)2 = a2b2
Merkwaardige producten(a + b)2 = a2 + 2ab + b2(a - b)2 = a2 - 2ab + b2(a + b)(a - b) = a2 - b2
Rekenregels met wortels(√(a))2 = a√(a) .√(b) = √(ab)√(a)/√(b) = √(a/b)
Regels voor machten
ap . aq = ap + q
(ap)q = ap . q
(ab)n = an . bn
ap/aq = ap - q
kwadraat afsplitsen |
| Hoofdstuk 6 | SOSCASTOA:sin(hellingshoek) = (Verticale verplaatsing) / (lengte parcours)sin(hoek A) = (Overstaande rechthoekszijde van hoek A) / (schuine zijde)cos(hoek A) = (Aanliggende rechthoekszijde van hoek A) / (schuine zijde)tan(hoek A) = (overstaande rechthoekszijde van hoek A) / (aanliggende rechthoekszijde van hoek A)
zijde . hoogte-methode:zijde . hoogte = zijde . hoogte |
| Hoofdstuk 7 | xtop = -b/2a |
| Hoofdstuk 8 | exponentiële groei: N = b . gtevenwichtsstand = (hoogste stand + laagste stand) / 2amplitude = hoogste stand - laagste standHyperbool: y = a/x (omgekeerd evenredig)

 |
| Hoofdstuk 9 | spreidingsbreedte = grootste getal - kleinste getalvermenigvuldigingsregel: p x qsomregel: p + q |
| Hoofdstuk 1 | halve competitie = 0,5 . n . (n-1)hele competitie = 1 . n . (n-1)afvalsysteem = n - 1 wedstrijden als er n teams meedoenn! = n . (n - 1) . (n - 2) . ... . 3 . 2 . 1 (! = faculteit)afspraak: 0! = 1het aantal permutaties van n dingen waarvan er p gelijk zijn en de rest verschillend, is n!/p!.

Combinaties
 |
| Hoofdstuk 2 | plottenminimummaximumextreme waarden (= uiterste waarden)
Lineaire forumlesy als functie van x --> y = ax + bp als functie van q --> p = aq + brc = a = Δy/Δx
Kwadratische formulesy = ax2 + bx + c
abc-formule: x = (-b +/- √(D)) / 2a, met D = b2 - 4acR = p . q
W = R - K (met R = opbrengst, p = prijs, q = aantal, K = kosten, W = winst) |
| Hoofdstuk 3 | Relatieve verandering = (nieuw - oud) / oud . 100%
Oppervlaktediagrammenopp(groot) = k . opp(klein)straal(groot) = √(k) . straal(klein)
(let op: bovenstaande wijkt af met de manier van de 2e klas, zie hoofdstuk 8)
Relatieve frequentie = frequentie / (totale frequentie) . 100%frequentiedichtheid van een klasse = frequentie van een klasse / klassenbreedte |
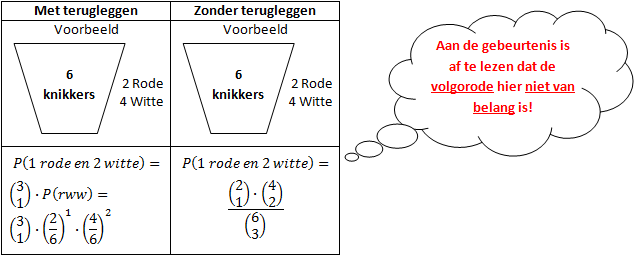
| Hoofdstuk 4 | Kansdefinitie van Laplace: P(gebeurtenis) = (aantal gunstige uitkomsten)/(aantal mogelijke uitkomsten)A en B zijn onafhankelijke gebeurtenissen als: P(A onder voorwaarde B) = P(A)
SomregelP(G1 of G2) = P(G1) + P(G2)
ComplementregelP(gebeurtenis) = 1 - P(complement gebeurtenis) |
| Hoofdstuk 5 | Machtsfunctiesevenredigevenredigheidsconstante
Machtsvergelijkingenmachtswortels, bereken exact de oplossingen van


Lineaire groeiN = a . t + b,
Exponentiële groeiN = b . gtgroeifactor gexponentieel vervalexponentiële afnamegroeipercentageverdubbelingstijd: gt = 2halveringstijd: gt = 0,5 |
| Hoofdstuk 6 | ProductregelP(G1 en G2) = P(G1) . P(G2)
SomregelP(G1 of G2) = P(G1) + P(G2)
ComplementregelP(gebeurtenis) = 1 - P(complement gebeurtenis)
bij onafhankelijke toevalsvariabelen: P(X = x onder voorwaarde Y = y) = PX = x) |
| Hoofdstuk 7 | Bij intervallengemiddelde verandering: Δy/Δxdifferentiequotiënt: Δy/Δxhelling van lijn AB: Δy/Δx = (yB - yA) / (xB - xA)richtingscoëfficiënt van lijn AB: Δy/Δx = (yB - yA) / (xB - xA)gemiddelde snelheid: Δs/Δt (hier is een eenheid vereist)
In één puntdifferentiaalquotiënt: dy/dxvia GR: [dy/dx]x=xA
Regels voor het differentiërenf(x) = a geeft f'(x) = 0f(x) = ax geeft f'(x) = af(x) = ax2 geeft f'(x) = 2axf(x) = axn geeft f'(x) = n . axn-1
Somregelf(x) = g(x) + h(x) geeft f'(x) = g'(x) + h'(x)
Notaties voor de afgeleide van y = f(x) zijn
dy/dx = f'(x) = d(f(x))/dx = y'(x) |
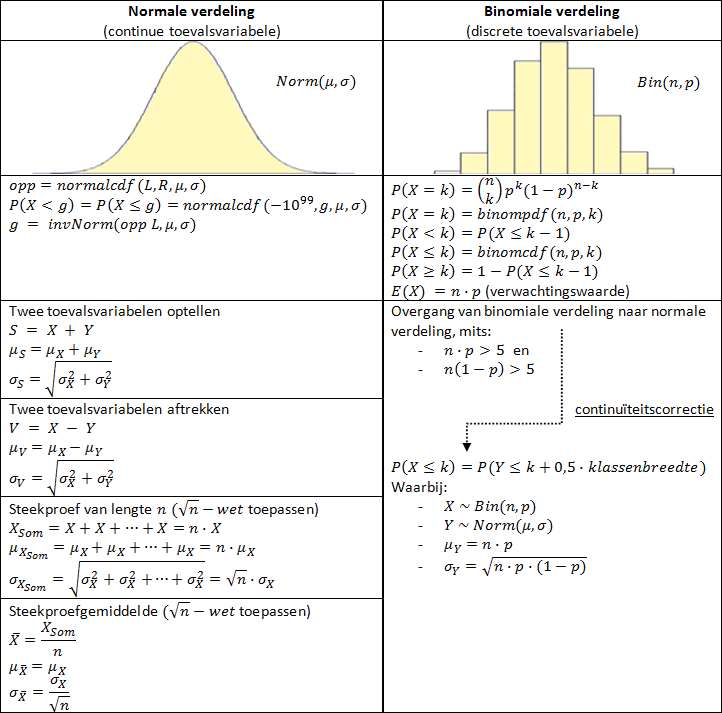
| Hoofdstuk 8 | opp = normalcdf(L, R, mu, sigma)grens = invNorm(opp L, mu, sigma) |
| Hoofdstuk 1 | 
abc-formule: x = (-b +/- √(D)) / 2a, met D = b2 - 4ac
Werkschema voor het oplossen van wortelvergelijkingen
1) Isoleren
2) kwadrateren
3) controleren
Regels voor gebroken vergelijkingenA/B = 0 geeft A = 0A/B = C/B geeft A = CA/B = A/C geeft A = 0 v B = CA/B = C/D geeft AD = BC
(controleer noemer ≠ 0)
Stelsels vergelijkingen oplossenelimineren door optellen of aftrekkenelimineren door substitutie
Werkschema ongelijkheden oplossen
1) vergelijking oplossen
2) schets grafiek(en)
3) x-as arceren
4) conclusie ongelijkheid |
| Hoofdstuk 2 | f(x) = ax + b (lineaire functie)a = Δy/Δxhorizontale lijn: y = averticale lijn: x = af(x) = ax2 + bx + c (kwadratische functie of tweedegraadsfunctie)
Hoe noteer je uitwerkingen bij gebruik GR?
1) vermeld ingevoerde formules
2) noteer gebruikte opties en geef resultaat
3) beantwoord de vraag
xtop = -b/2ay = axn --> translatie (p,q) --> y = a(x - p)n + qgebroken functies: f(x) = a/x (hyperbool) |
| Hoofdstuk 3 | Bij intervallengemiddelde verandering: Δy/Δxdifferentiequotiënt: Δy/Δxhelling van lijn AB: Δy/Δx = (yB - yA) / (xB - xA)richtingscoëfficiënt van lijn AB: Δy/Δx = (yB - yA) / (xB - xA)gemiddelde snelheid: Δs/Δt (hier is een eenheid vereist)
In één puntvia GR: [dy/dx]x=xA
Differentiërenf(x) = a geeft f '(x) = 0f(x) = ax geeft f '(x) = af(x) = axn geeft f '(x) = naxn-1f(x) = c . g(x) geeft f '(x) = c . g'(x)f(x) = g(x) + h(x) geeft f '(x) = g'(x) + h'(x) (somregel) |
| Hoofdstuk 4 | 
Rekenregels met wortels√(a) .√(b) = √(ab)√(a)/√(b) = √(a/b)√((a)2) = |a|
Merkwaardige producten
(a + b)(a - b) = a2 - b2
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
SOSCASTOA
Sinusregela/sin(α) = b/sin(β) = c/sin(γ)
Cosinusregela2 = b2 + c2 - 2bc cos(α)b2 = a2 + c2 - 2ac cos(β)c2 = a2 + b2 - 2ab cos(γ)
Oppervlakte vlakke figurenopp(parallellogram) = b . hopp(driehoek) = 0,5 . b . hopp(cirkel) = pi . r2
a2 + b2 = c2 (Stelling van Pythagoras) |
| Hoofdstuk 5 | y = gx (exponentiële formule)N = b . gt (exponentiële formule)N = at + b (lineaire formule)y = glog(x) (logaritmische formule)L = 10 log(I/I0) (formule voor geluidsniveau)gt = 2 (verdubbelingstijd)gt = 1/2 (halveringstijd)
 |
| Hoofdstuk 6 | Voor draaiingshoek α van het punt P(xP, yP) op de eenheidscirkel geldtsin(α) = yPcos(α) = xPtan(α) = yP/xP
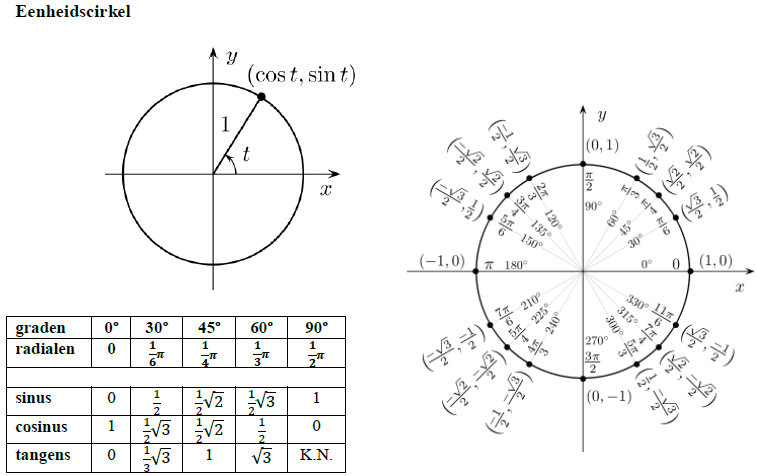
sin(A) = C geeft A = sin-1(C)cos(A) = C geeft A = cos-1(C)sin(A) = sin(A) geeft A = B + k.2 pi of A = pi - B + k.2 picos(A) = cos(A) geeft A = B + k.2 pi of A = - B + k.2 pi
y = a + b sin(c(x - d)) & y = a + b cos(c(x - d))a = evenwichtsstand = (minimum + maximum)/2|b| = amplitudec = 2 pi/perioded = verplaatsing
| b > 0 | b < 0 |
|---|
| sin | stijgend door het beginpunt | dalend door het beginpunt |
|---|
| cos | het beginpunt is het hoogste punt | het beginpunt is het laagste punt |
|---|
|
| Hoofdstuk 7 | Differentiërenf(x) = a geeft f '(x) = 0f(x) = ax geeft f '(x) = af(x) = axn geeft f '(x) = naxn-1f(x) = c . g(x) geeft f '(x) = c . g'(x)f(x) = g(x) + h(x) geeft f '(x) = g'(x) + h'(x) (somregel)
Regels voor het differentiëren
Somregels(x) = f(x) + g(x) geeft s'(x) = f '(x) + g'(x)
productregelp(x) = f(x) . g(x) geeft p'(x) = f '(x) . g(x) + f(x) . g'(x)
quotiëntregelq(x) = t(x)/n(x) geeft q'(x) = (n(x) . t'(x) - t(x) . n'(x))/(n(x))2
kettingregeldy/dx = dy/du . du/dx
 |
| Hoofdstuk 8 | Stelling van Pythagorasa2 + b2 = c2
Werkschema voor het bewijzen van een stelling
1) gegeven
2) te bewijzen
3) bewijs (vermeld alle definities en stellingen) |
| Hoofdstuk 9 | 
Sinusoïden: y = a + b sin(c(x - d))a = evenwichtsstand = (maximum + minimum)/2b = amplitudec = 2 pi/perioded = verplaatsing |
Hoofdstuk 10
Hoofdstuk 11 | machtsfunctie: f(x) = axntranslatiebeeldgrafiekvermenigvuldigen t.o.v. de x-aswotelfunctiebeginpuntdomeinbereikgebroken functieshyperboolhorizontale asymptootverticale asymptootexponentiële functieslogaritmische functiesgrondtal van de logaritmeinverse functielogaritmische schaalverdelinglogaritmisch papierdubbellogaritmisch papier
KruisproductenA/B = C geeft A = BCA/B = C/D geeft AD = BCgA = gB geeft A = B


wisC:
Nietlogaritmische functiesgrondtal van de logaritmeinverse functielogaritmische schaalverdelinglogaritmisch papierdubbellogaritmisch papier
Welformules met twee variabelenlogistische groeiverzadigingsniveau |
Hoofdstuk 11
Hoofdstuk 10 | 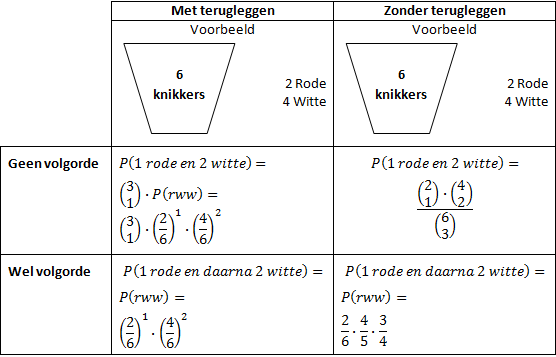
Kansdefinitie van LaplaceP(gebeurtenis) = (aantal gunstige uitkomsten)/(aantal mogelijke uitkomsten)
SomregelP(G1 of G2) = P(G1) + P(G2)
ComplementregelP(gebeurtenis) = 1 - P(complement gebeurtenis)
Optellen van breuken
Gelijknamige breuken optellen: A/B + C/B = (A+C)/B
Niet-gelijknamige breuken optellen: A/B + C/D = (AD + BC) / (BD)
Speciaal geval: A + B/C = (AC + B) / C
Breuk . breuk = (teller . teller) / (noemer . noemer)
Vermenigvuldigen van breuken
A/B . C/D = AC/(BD)
Speciaal geval: A . B/C = AB/C en ook A/C . B = AB/C en A . B . 1/C = AB/C
Delen door een breuk
'Delen door een breuk is vermenigivuldigen met het omgekeerde van de breuk', dus A/(B/C) = A . C/B = AC/B
Haakjes wegwerken
a(b + c) = ab + ac
(a + b)(c + d) = ac + ad + bc + bd
Binomiaal kansexperiment
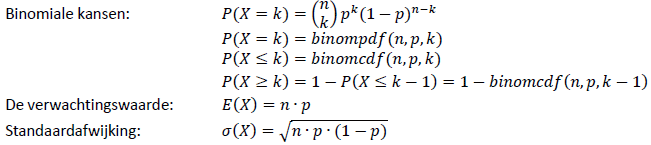
Verwachtingswaarde & standaardafwijking
E(X) = x1 . P(X = x1) + x2 . P(X = x2) + ... + xn . P(X = xn)
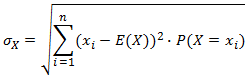 (Alleen kennen via 1-Var Stats) (Alleen kennen via 1-Var Stats)
Som van toevalsvariabelen
E(X + Y) = E(X) + E(Y)
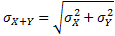 |
Hoofdstuk 12
niet voor wisC! | Differentiequotiënt: Δy/ΔxDifferentiaalquotiënt: dy/dx
Regels voor het differentiërenf(x) = a geeft f'(x) = 0f(x) = ax geeft f'(x) = af(x) = axn geeft f'(x) = n . axn-1
Notaties voor de afgeleide van y = f(x)
dy/dx = f'(x) = d(f(x))/dx = y'(x)
Marginale Kosten, Opbrengst, WinstMK = K' = dK/dqMR = R' = dR/dqMW = W' = dW/dq
Gemiddelde Kosten, Opbrengst, WinstGK = K/qGR = R/qGW = W/q
Variabelen in het voorraadmodeln: het aantal bestellingen per jaarVK: de voorraadkosten per jaar in euro'sBK: de bestelkosten per jaar in euro'sTK: de totale kosten in euro's, dus TK = VK + BK
Kettingregeldy/dx = dy/du . du/dx |
Hoofdstuk K
Dit is H12 voor wisC! | Grafenmaximale verbondenheid: aantal verbindingen is n nCr 2 [oftewel een halve competitie: 0,5 . n . (n-1)]Minimale verbondenheid: aantal verbindingen is n - 1 |
| Hoofdstuk 9 | 

gA = gB geeft A = Bf(x) = ex geeft f '(x) = exf(x) = ax geeft f '(x) = ax . ln(a)f(x) = ln(x) geeft f '(x) = 1/xf(x) = glog(x) = 1/(x ln(g)) |
| Hoofdstuk 10 | 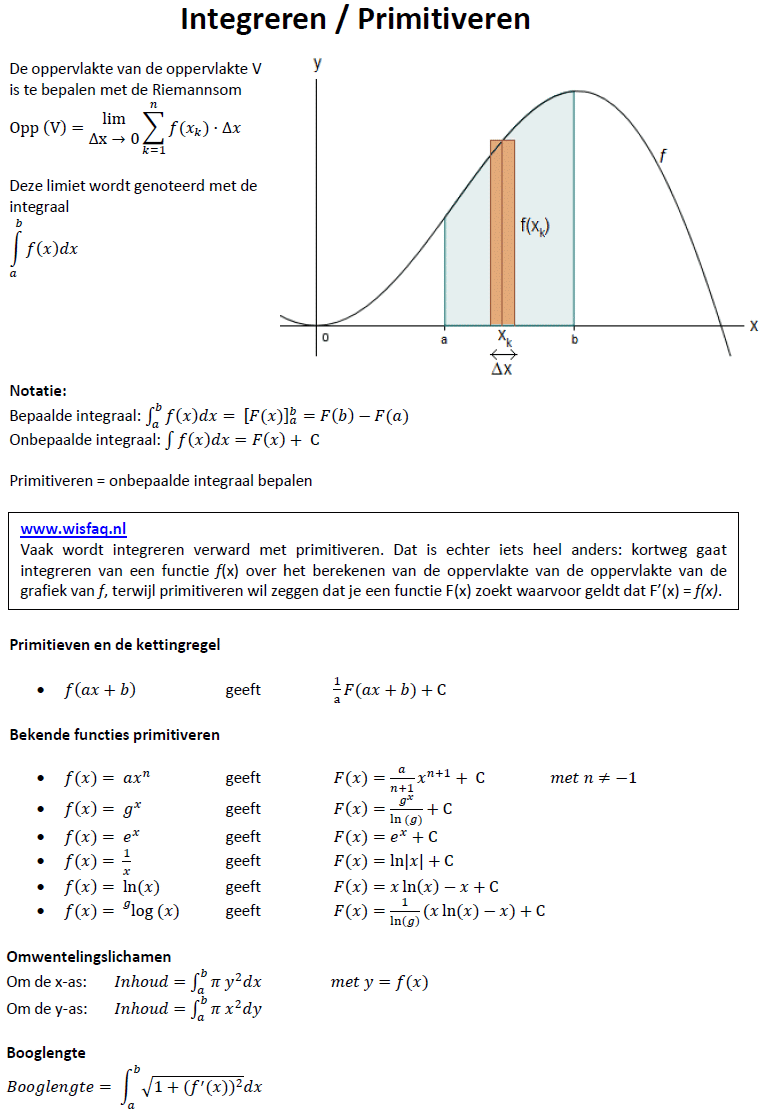 |
| Hoofdstuk 11 | 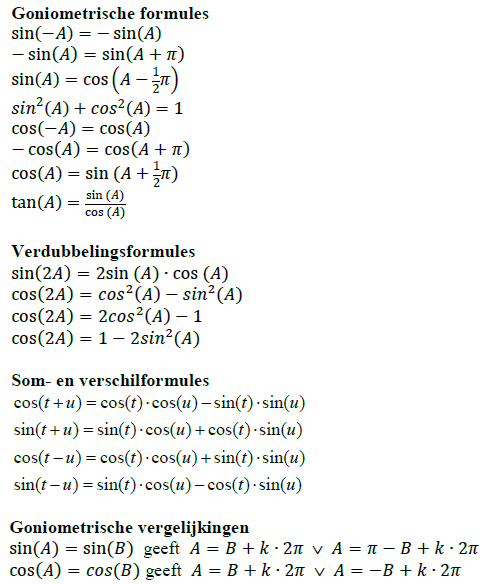
f(a - p) = f(a + p) (lijnsymmetrie: algemeen)f(-p) = f(p) (lijnsymmetrie: in y-as)f(a - p) + f(a + p) = 2b (puntsymmetrie: algemeen)f(-p) + f(p) = 0 (puntsymmetrie: in oorsprong)
Differentiërenf(x) = sin(x) geeft f '(x) = cos(x)f(x) = cos(x) geeft f '(x) = sin(x)f(x) = tan(x) geeft f '(x) = 1/cos2(x) en f '(x) = 1 + tan2(x)
Primitiverenf(x) = sin(x) geeft F(x) = -cos(x) + Cf(x) = cos(x) geeft F(x) = sin(x) + C
omloopstijd: Thoeksnelheid |ω| = 2pi/Tomloopstijd = periode |
| Hoofdstuk K | f '(x) = df(x)/dxdf(x) = f '(x)dxf(x)dx = dF(x)dy/dx = dy/du . du/dx (kettingregel)f(g(x)) . g'(x) dx = f(g(x)) d(g(x)) = f(u) du = d(F(u) + C) = d(F(g(x)) + C) (substitutiemethode)f(x) = tan(x) geeft F(x) = -ln|cos(x)| + Cf '(x) . g(x) dx = g(x) df(x) = d(f(x) . g(x)) - f(x) dg(x) (partieel integreren)
Werkschema partieel integreren
1) Noem de functie om eerst te primitiveren f 'en de andere functie g
2) Herleid f 'g dx tot g df
3) Gebruik g df = dfg -f dg
4) Herleid dfg - f dg tpt d(fg - ...)
Cyclometrische functiesf(x) = 1/(x2 + 1) geeft F(x) = arctan(x) + Cf(x) = 1/√(1 - x2) geeft F(x) = arsin(x) + C |
Keuzeonderwerp:
Kansrekening | Kansdefinitie van Laplace: P(gebeurtenis) = (aantal gunstige uitkomsten)/(aantal mogelijke uitkomsten)n! = n . (n - 1) . (n - 2) . ... . 3 . 2 . 1n nPr k = n!/(n - k)!n nCr k = n!/k! . (n - k)!aantal = nk (rangschikking met herhaling)

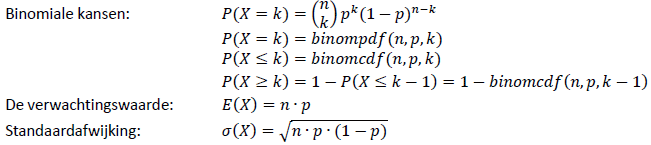
opp = normalcdf(L, R, mu, sigma)grens = invNorm(opp L, mu, sigma) |
Hoofdstuk 13
Dit is H14 voor wisC! | 
Kansdefinitie van LaplaceP(gebeurtenis) = (aantal gunstige uitkomsten)/(aantal mogelijke uitkomsten)
SomregelP(G1 of G2) = P(G1) + P(G2)
ComplementregelP(gebeurtenis) = 1 - P(complement gebeurtenis)
 |
Hoofdstuk 14
Dit is H13 voor wisC!
(zie onder) | Lineaire functiey = ax + ba = Δy/Δxverticale lijn: x = ahorizontale lijn: y = avergelijking van de vorm ax + by = cstelsels vergelijkingen oplossen
Kwadratische formulekwadratische vergelijkingen oplossen
Vergelijkingen van de vormAB = 0 geeft A = 0 v B = 0AB = AB geeft A = 0 v B = CA2 = B2 geeft A = B v A = -B√(A) = B geeft A = B2
Gebroken vergelijkingenA/B = C geeft A = BCA/B = 0 geeft A = 0A/B = C/D geeft AD = BC
Herleiden van breuken
OptellenA/B + C/D = (AD + BC) / (BD)A + B/C = A/1 + B/C = (AC + B) / C
OptellenA/B . C/D = (AC)/(BD)A . B/C = (AB)/C
DelenA/(B/C) = A . C/B = AC/B(A/B)/C = A/(BC)
WisseleigenschapUit C = A/b volgt B = A/C
Exponentiële groeiN = b . gt


wisC
Lineaire functiey = ax + ba = Δy/Δxverticale lijn: x = ahorizontale lijn: y = a
Exponentiële groeiN = b . gt

 |
Hoofdstuk 15
Compleet ander
hoofstuk voor wisC!
(zie onder) | 
wisCprocentuele verandering: (model - werkelijkheid) / werkelijkheid . 100%machtsfunctiesgebroken functieslogistische functieswortelfunctiesformules met twee of meer variabelen
evenredigy is evenredig met x2 --> y = ax2
Formules in de economiep = aq + b (prijs-afzet-functie)R = p . q (opbrengst)W = R - K (winst)
Vergelijkingen oplossenA . B = 0 geeft A = 0 v B = 0√(A) = B geeft A = B2√(AB) = √(A) . √(B)
Gebroken vergelijkingenA/B = C geeft A = BCA/B = 0 geeft A = 0A/B = C/D geeft AD = BC
Herleiden van breuken
OptellenA/B + C/D = (AD + BC) / (BD)A + B/C = A/1 + B/C = (AC + B) / C
OptellenA/B . C/D = (AC)/(BD)A . B/C = (AB)/C
DelenA/(B/C) = A . C/B = AC/B(A/B)/C = A/(BC)
Wisseleigenschapuit C = A/b volgt B = A/C
Bij intervallengemiddelde verandering: Δy/Δxdifferentiequotiënt: Δy/Δxhelling van lijn AB: Δy/Δx = (yB - yA) / (xB - xA)richtingscoëfficiënt van lijn AB: Δy/Δx = (yB - yA) / (xB - xA)gemiddelde snelheid: Δs/Δt (hier is een eenheid vereist)
In één puntvia GR: [dy/dx]x=xArichtingscoëfficiënt van de raaklijn van de grafiek in Ade helling van de grafiek in Ade snelheid waarmee y verandert voor x = xA |
| Hoofdstuk 16 | evenredig/ omgekeerd evenredigy is evenredig met x2 --> y = ax2y is omgekeerd evenredig met x2 --> y = a/x2
Minimale/maximale snelheidd/dx(dy/dx) = 0
Bij intervallenGemiddelde verandering: Δy/ΔxDifferentiequotiënt: Δy/ΔxHelling van lijn AB: Δy/Δx = (yB - yA) / (xB - xA)Richtingscoëfficiënt van lijn AB: Δy/Δx = (yB - yA) / (xB - xA)Gemiddelde snelheid: Δs/Δt (hier is een eenheid vereist)
In één puntDifferentiaalquotiënt: dy/dxVia GR: [dy/dx]x=xA
Notaties voor de afgeleide van y = f(x) zijn
dy/dx = f'(x) = d(f(x))/dx = y'(x)
Regels voor het differentiërenf(x) = axn geeft f '(x) = n . axn - 1g(x) = a . f(x) geeft g'(x) = a . f '(x)
Somregels(x) = f(x) + g(x) geeft s'(x) = f '(x) + g'(x)
productregelp(x) = f(x) . g(x) geeft p'(x) = f '(x) . g(x) + f(x) . g'(x)
quotiëntregelq(x) = f(x)/g(x) geeft q'(x) = (g(x) . f '(x) - f(x) . g'(x))/(g(x))2
kettingregeldy/dx = dy/du . du/dx
Stelling van Pythagorasa2 + b2 = c2 |


















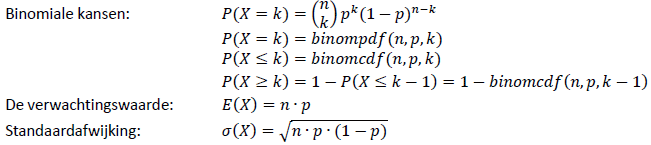
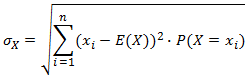 (Alleen kennen via 1-Var Stats)
(Alleen kennen via 1-Var Stats)